Derive Steady Flow Energy Equation
The equation for an evaporating surface can be written as. Once this temperature distribution is known the conduction heat flux at any point in the material or.

Engineering Thermodynamics Steady Flow Energy Equation S F E E
Web All fluxes of energy should be considered when deriving an energy balance equation.
. R n - G - l ET-H 0 1 where R n is the net radiation H the sensible heat G the soil heat flux and l ET the latent heat flux. Friedmann form and Crocco form. Web ProofIf A is a constant matrix Φt t 0 e Att 0.
Web According to the textbook I copied it from l is a pathline in the flow. Hence Φt s e Ats and 64 reduces to 41We defer the proof of the general case where At depends on t until later in this section. 1 The solution to the mathematical model equations gives the velocity field.
Web Constant Thermal Conductivity and Steady-state Heat Transfer Poissons equation. Web To explain flux first there must be a quantity q that can flow or move such as energy mass electric charge momentum number of molecules etc. Web We shall derive Bernoullis equation by starting with the conservation of energy equation.
Web April 12th 2019 - Documentation for MATLAB code For heat transfer our balance equation is one of energy one dimensional and two dimensional heat flow equation in steady Modeling and Simulation of a 2 2 2 1 2 y T t x T The ADI method can be used for parabolic equations in Implicit Matlab Code MILAMIN MATLAB based finite element Jessica King. The duo focus on a class of continuous processes where the system interacts with a thermal environment that is forgetful. Web The momentum equation is used in open channel flow problems to determine unknown forces F acting on the walls or bed in a control volumeIn comparison to the energy equation that deals with scalar quantities such as mass m pressure P and velocity magnitude V the momentum equation deals with vector quantities such as velocity.
The environment initially in equilibrium has a brief energy exchange with the. Studying an enzymes kinetics in this way can reveal the catalytic mechanism of this enzyme its role in metabolism how its activity is controlled. Of the fluid in the modeled domain.
In the usual case of small potential field simply. Web where M i is the relative molar mass kg mol-1 of species i. Web The heat conduction equation is a partial differential equation that describes heat distribution or the temperature field in a given body over timeDetailed knowledge of the temperature field is very important in thermal conduction through materials.
Ht2 - ht1 q - wsh where ht is the total enthalpy of the fluid q is the heat transfer into the fluid and wsh is. Web They also derive a family of entropy-production inequalities that supplant the standard second law by a more fine-grained requirement. Additional simplifications of the general form of the heat equation are often possible.
The various terms can be either positive or negative. The diffusive mass flux of each species is in turn expressed based on the gradients of the mole or mass fractions using multi-component diffusion coefficients D ikThese are symmetric so that an n-component system requires nn-12 independent coefficients to parameterize the rate. Again lets look at a concrete example.
Web For instance a flow field is characterized by balance in mass momentum and total energy described by the continuity equation the Navier-Stokes equations and the total energy equation. Web Enzyme kinetics is the study of the rates of enzyme-catalysed chemical reactionsIn enzyme kinetics the reaction rate is measured and the effects of varying the conditions of the reaction are investigated. In Continuity Equation Flux is of Two.
Positive R n supplies energy to the. When they derive Bernoullis from it the assumption is the flow is steady and the local acceleration fracpartial Vpartial t 0. For example under steady-state conditions there can be no change in the amount of energy storage Tt 0.
Then they say that with this assumption the pathline becomes a streamline s and the derivatives become. Web From here it is easy to derive the explanation for why any non-zero number raised to the zero power equals 1. Again lets look at a concrete example.
Let us assume ρ is the volume density of this quantity q that is the amount of q per unit volume. Equation 64 is the solution to the general initial-value problem given by 58It should be noted however that since Φt t 0 is not explicitly known xt will not be. Web Plasma Physics and Controlled Fusion is a monthly publication dedicated to the dissemination of original results on all aspects experimental and theoretical of the physics of hot highly ionized plasmas.
The way by which this quantity q is flowing is described by its flux. By substituting the pressure gradient with the entropy and enthalpy gradient. Web That is the energy balance for a steady inviscid flow in an external conservative field states that the sum of the total enthalpy and the external potential is constant along a streamline.
Assuming a steady inviscid flow we have a simplified conservation of energy equation in terms of the enthalpy of the fluid.
Derive Steady Flow Energy Equation Sarthaks Econnect Largest Online Education Community

Application Of The Steady Flow Energy Equation Sfee Youtube
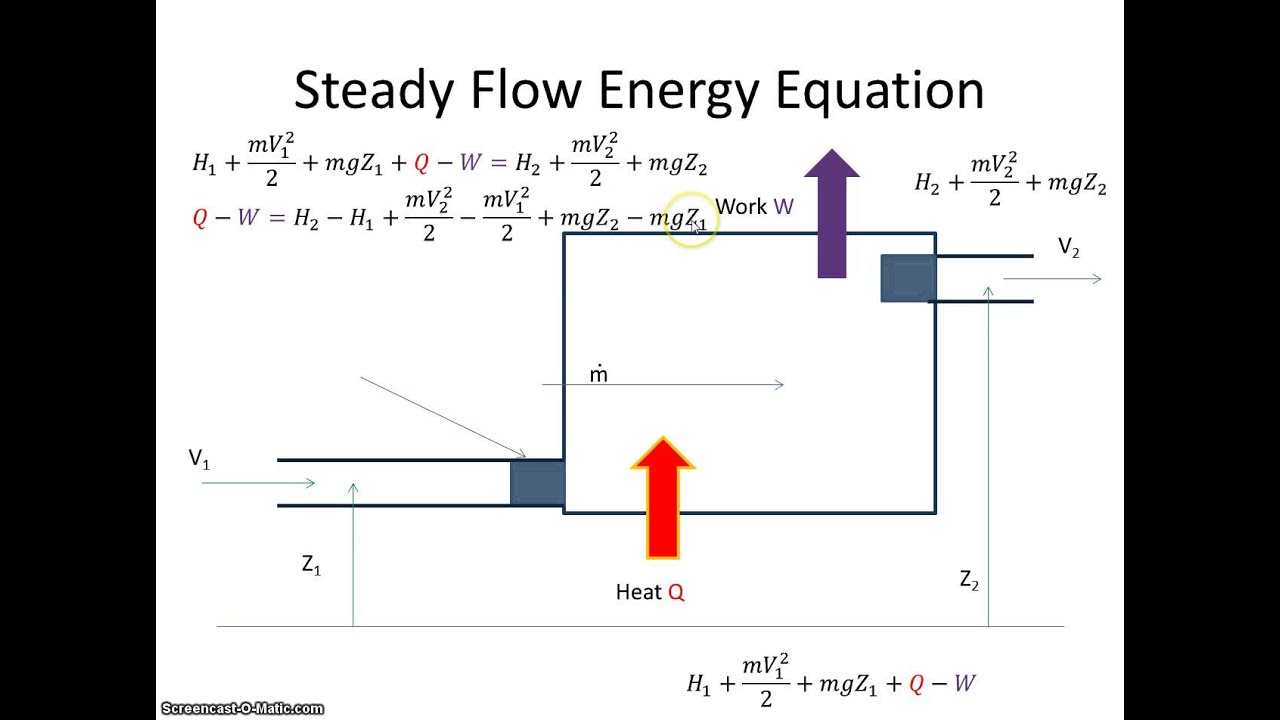
Steady State Energy Equation Youtube

Steady Flow Energy Equation S F E E And Its Applications Part 1 Youtube
No comments for "Derive Steady Flow Energy Equation"
Post a Comment